De ultieme tegel is eindelijk gevonden

Posted on March 30, 2023 by admin

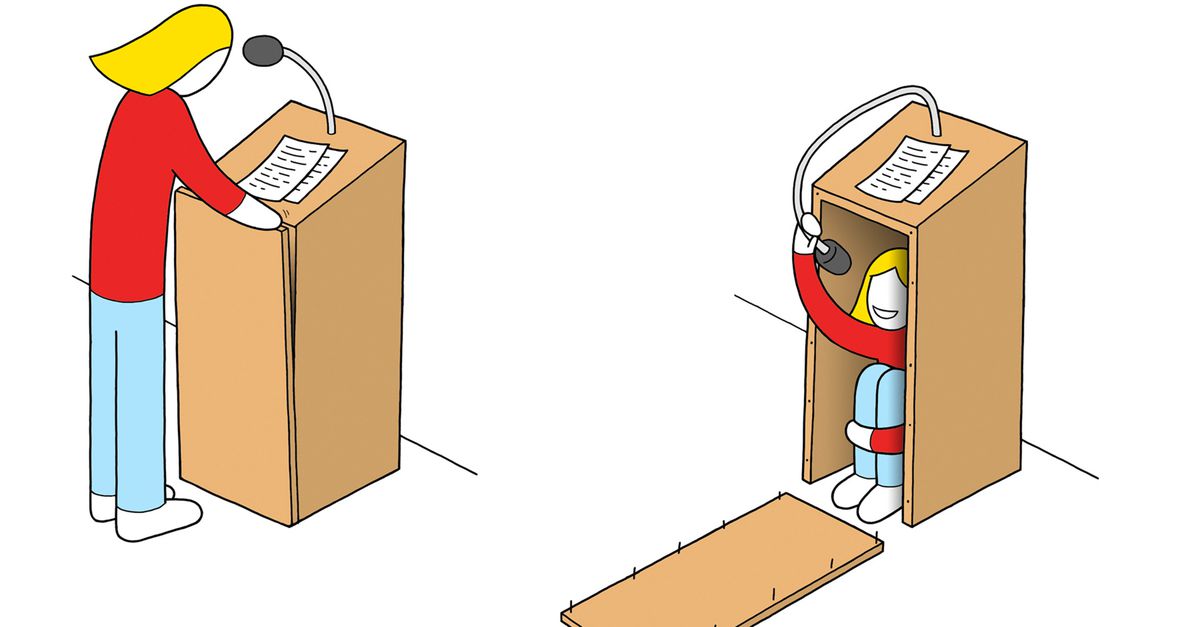
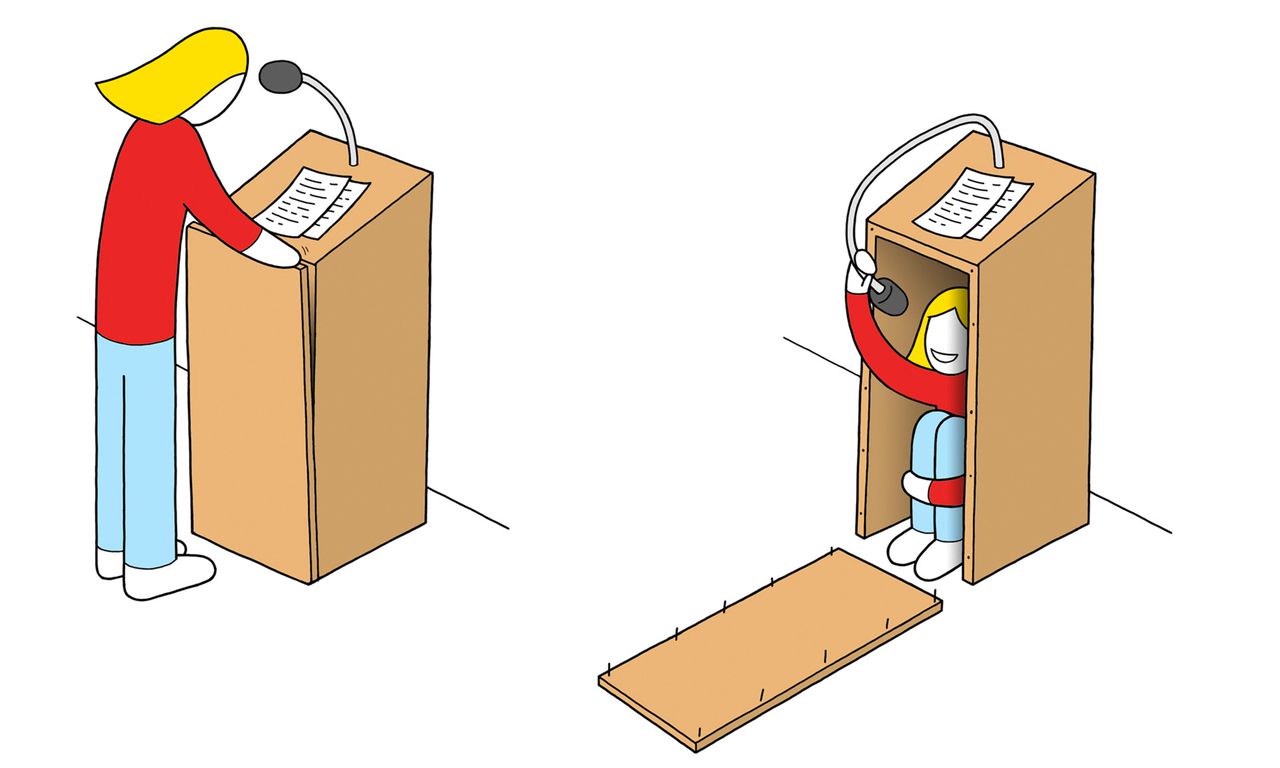
Een ‘einstein’ is een vorm waarmee een oneindig vlak uitsluitend onregelmatig kan worden betegeld. De donkerblauwe tegels zijn gespiegeld. De lichtblauwe zijn de tegels die direct aan een gespiegelde tegel grenzen.

N.B. Het kan zijn dat elementen ontbreken aan deze printversie.

Wiskunde Wiskundigen hebben een bijzondere tegel ontdekt. Het begon met een liefhebber die gewoon wat aan het uitproberen was.

Alex van den Brandhof

30 maart 2023 om 9:12

Leestijd 3 minuten

Wiskundigen hebben een tegel ontdekt die een vlak naadloos kan vullen. Bijzonder eraan is dat die betegeling uitsluitend op een niet-herhalende manier tot stand kan worden gebracht. De vondst baart opzien, want het was onbekend of zulke tegels bestaan.

De meeste betegelingen hebben een herhalend patroon, zoals vierkanten in een schaakbordpatroon, of zeshoeken in de bekende honingraat. Zo’n ‘schuifsymmetrische’ betegeling heet periodiek: je kunt de betegeling zodanig verschuiven dat die er ná de verschuiving precies zo uitziet als ervóór. Het is niet moeilijk om een vlak aperiodiek te betegelen: knip van een schaakbordpatroon elk vierkant zo door dat twee identieke rechthoeken ontstaan – sommige horizontaal, andere verticaal, totaal willekeurig. Door die willekeur verdwijnt alle regelmaat.

Al gauw ontkracht

De uitdaging is: bestaan er ook tegels, of verzamelingen van tegels, die een oneindig vlak alléén op een aperiodieke manier kunnen betegelen? In 1961 publiceerde de wiskundige Hao Wang een artikel waarin hij het vermoeden uitte dat het antwoord nee is. Maar dat vermoeden werd al gauw ontkracht. De eerste betegeling die werd gevonden, was gebaseerd op een set van 20.426 verschillende tegels.

Wiskundigen wilden weten of ze dat aantal konden verlagen. Halverwege de jaren zeventig bewees de wis- en natuurkundige Roger Penrose dat er twee verrassend eenvoudige vormen bestaan – hij noemde ze ‘vliegers’ en ‘pijlen’ – waarmee een echte aperiodieke betegeling mogelijk is.

De twee tegels van Penrose riepen de vraag op: zou er een enkele, slim gevormde tegel kunnen zijn die precies past? In 2011 vonden Joshua Socolar en Joan Taylor een vorm die in de buurt komt, maar die bestaat uit losse stukjes en voldoet daarmee niet aan de definitie van ‘tegel’.

Met de Socolar-Taylor-vorm kan een oneindig vlak worden betegeld, maar deze vorm is niet één samenhangend geheel en daarom geen ‘tegel’.

Een grote verrassing

Het definitieve antwoord kwam vorige week van David Smith, Joseph Myers, Craig Kaplan en Chaim Goodman-Strauss. Ja, er bestaat een samenhangende vorm, een echte tegel dus, waarmee een oneindig vlak wél aperiodiek maar niet periodiek kan worden gevuld. Een ‘einstein’, zoals wiskundigen zeggen.

Een grote verrassing, opwinding op sociale media. „Ik had niet gedacht dat er een einstein zou bestaan”, reageert Jaap Scherphuis, een Delftse maker van software voor puzzelontwerpers. De tegel is zelfs verrassend simpel: een dertienhoek, met hoeken van 90, 120, 240 en 270 graden. Scherphuis: „Het is bijzonder dat de tegel is gebaseerd op een regelmatig patroon van opgedeelde zeshoeken, en niet op de vijfvoudige draaisymmetrie die wordt gebruikt in Penrosetegels.”

David Smith, uit Yorkshire in Engeland, is de ontdekker van de einstein. Hij is geen professioneel wiskundige, maar als liefhebber van patronen was hij gewoon wat aan het uitproberen. Met behulp van een programma van Scherphuis lukte het hem om een groot vlak redelijk sluitend te betegelen met de dertienhoek. Niet helemaal naadloos, maar Smith gaf niet op. Handmatig wist hij de gaten te vullen, waarop hij zich begon af te vragen of deze tegel een antwoord zou kunnen zijn op het einsteinprobleem.

Smith mailde Craig Kaplan, informaticus van de University of Waterloo in Canada. Toen begon het échte onderzoek naar de tegel. De aanpak was om met één tegel te beginnen en die te omringen met een laag tegels. De volgende stap was om daar opnieuw een ring omheen te leggen. En dan nóg een ring, net zo vaak, totdat dat niet meer lukt. Het ‘Heeschgetal’ van een tegelvorm is het maximale aantal ringen dat mogelijk is. Het hoogst bekende Heeschgetal is 6: in 2020 werd een vorm gevonden die omringd kan worden met zes lagen van diezelfde vorm, maar niet met zeven.

Een tegel met Heeschgetal 3: rond de centrale tegel (zwart) kunnen drie ringen naadloos worden gelegd, maar niet meer. Elke ring heeft een andere kleur, waarbij de twee tinten de originele en gespiegelde oriëntatie aangeven.

Overweldigende reacties

Met een zogeheten ‘SAT-solver’ vond Kaplan zestien lagen om de dertienhoekige tegel van Smith. „Op dat moment was ik ervan overtuigd dat de tegel een oneindig vlak kan betegelen”, mailt hij. Zijn argument: als dat niet mogelijk was geweest, was het Heeschgetal van de tegel minstens 16 geweest. Dat leek hem uitgesloten: bijna drie keer zo groot als het huidige record. „Bovendien geloofde ik dat de betegeling aperiodiek is, vanwege de wilde structuren die de SAT-solver vond.”

In hun paper – dat nog niet officieel is gepubliceerd maar wel al overweldigende reacties heeft gekregen – bewijzen de onderzoekers dat de tegel inderdaad vlakvullend is en óók dat die betegeling aperiodiek is. Groepjes tegels worden samengevoegd tot grotere clusters, ‘metategels’ genaamd. Die metategels worden op hun beurt gerangschikt tot ‘supertegels’. Dat proces wordt eindeloos herhaald, waardoor een steeds groter deel van het vlak wordt bedekt. Het is een fractalachtig proces. In de limiet is het hele, oneindige vlak gevuld.

Maar daarmee is de klus nog niet geklaard. De tegel is pas een echte einstein als een periodieke betegeling onmogelijk is. Het bewijs daarvan is gebaseerd op een gloednieuw idee en maakt gebruik van het feit dat de tegel deel uitmaakt van een heel continuüm van vormen, die allemaal einsteins zijn. „We hopen dat dit idee in de toekomst verder onderzoek zal stimuleren”, aldus Kaplan.

Zes gewonden bij grote raketaanval van Hezbollah op Israël

admin
November 25, 2024
0

Bij luchtaanvallen van Hezbollah op meerdere plekken in Israël zijn in de nacht van zondag op maandag zeker zes personen gewond geraakt. Hezbollah vuurde zondagavond ruim 250 rakketten af, het grootste aantal in lange tijd. Dat melden internationale persbureaus. Het Israëlische leger heeft de meeste raketten naar eigen zeggen onderschept. De projectielen bereikten onder meer de buurt van Tel Aviv.

Eerder op zondag vuurde Hezbollah ook al tientallen raketten af op meerdere doelen in Israël. De aanval volgt op het Israëlische bombardement van vrijdag- op zaterdagnacht op een dichtbevolkte woonwijk in het centrum van de Libanese hoofdstad Beiroet. Daarbij zijn volgens Libanese autoriteiten zeker 84 personen gedood, ruim 213 anderen raakten gewond. Ook zondag heeft Israël verschillende aanvallen op Libanon uitgevoerd.

Verschillende Israëlische media, waaronder de publieke omroep Kan en de door de regering geboycotte krant Haaretz, hebben zondagavond gepubliceerd over een akkoord „op hoofdlijnen” over een mogelijk staakt-het-vuren tussen Hezbollah en Israël, met ruggensteun van de Verenigde Staten. Het akkoord zou nog niet definitief zijn. Onderhandelingen over gevechtspauzes zijn het afgelopen jaar zeer kwetsbaar gebleken.

Het Amerikaanse nieuwsmedium Axios meldt op basis van twee Amerikaanse en twee Israëlische bronnen dat de Amerikaanse onderhandelaar Amos Hochstein zaterdag druk zou hebben gezet op Israël. Hochstein, die al een jaar medieert tussen beide partijen, zou de Israëlische premier Benjamin Netanyahu hebben laten weten dat zich terug te trekken als onderhandelaar als Israël niet spoedig stappen zou zetten richting een akkoord met Hezbollah.

Zondagavond is rook te zien boven de Libanese hoofdstad Beiroet.

Kabinet wil aftrek hypotheekrente verhogen voor midden- en hoge inkomens

admin
November 25, 2024
0

Goedemorgen, welkom bij het economieblog van 25 november.

De aftrek van de hypotheekrente is een heikel punt. Toch is het kabinet van plan om de regels te veranderen: middeninkomens en hoge inkomens mogen straks meer aftrekken dan lage inkomens, meldt Het Financieele Dagblad. De Eerste Kamer kan er nog een stokje voor steken.

De verwachting is dat de regering-Biden nog deze week strengere exportmaatregelen voor Chinese chipbedrijven aankondigt. Het zou gaan om honderden chipmakers in China die geen geavanceerde apparatuur uit het Westen meer mogen importeren. Wat dat voor ASML en ASM International betekent is niet zeker. Nog voor Thanksgiving (donderdag) zouden de regels bekend moeten worden.

De Italiaanse bank UniCredit doet een bod van 10 miljard dollar op zijn Italiaanse concurrent, Banco BPM. De Financial Times ziet dit als het teken van een nieuwe consolidatietrend, om met grotere Europese banken beter te concurreren met banken uit de VS en Azië.

Bloomberg meldt dat beurzen positief reageren op de keuze van Scott Bessent als voorgestelde kandidaat-minister van Financiën in de regering-Trump. Geen verrassing: hij is van plan de belastingen te verlagen, vertelde hij de The Wall Street Journal.

Door de populariteit van streamingdiensten zijn burgers minder goed op de hoogte van het nieuws, waarschuwt het Commissariaat voor de Media

admin
November 25, 2024
0

Omdat Nederlanders steeds minder naar traditionele ‘lineaire’ televisie kijken en steeds vaker naar streamingdiensten, dreigen ze minder geïnformeerd te raken over wat er in de wereld gebeurt. Dat stelt het Commissariaat voor de Media in de Mediamonitor 2024, een jaarlijks rapport over trends in mediagebruik dat deze maandag is gepubliceerd.

„Internationale sociale media en streamingdiensten bepalen steeds meer hoe we informatie consumeren, terwijl het huidige Nederlandse aanbod onder druk staat”, stelt de voorzitter van de toezichthouder, Amma Asante, in het rapport. „Hoe zorgen we ervoor dat betrouwbare en relevante informatie zichtbaar en toegankelijk blijft?”

In een begeleidend persbericht noemt het Commissariaat deze ontwikkeling „zorgelijk omdat Nederlandse televisiezenders niet alleen burgers informeren, maar ook een verbindende rol spelen in de samenleving. Streamingdiensten kunnen deze functies niet overnemen, omdat zij geen nieuws en actualiteiten aanbieden, en slechts een beperkt Nederlands aanbod hebben.’’ Streamingdiensten bieden vooral films en series aan.

Sociale media zouden een grotere rol kunnen spelen bij het informeren van burgers, „maar alleen als betrouwbare journalistiek beter zichtbaar en vindbaar wordt. Dit vraagt om gerichte actie van zowel wetgevers als mediabedrijven.’’

Nog geen twee uur

In 2013 keken Nederlanders gemiddeld nog bijna drie uur per dag naar lineaire televisie (programma’s die bekeken worden op het moment waarop ze worden uitgezonden). Tien jaar later is dat nog geen twee uur, stelt het rapport.

Tussen 2013 en 2023 is het aantal mensen dat op een willekeurige dag via televisiezenders met nieuws en actualiteiten in aanraking komt fors gedaald. Bereikten nieuws en actualiteiten in 2013 dagelijks op die manier nog 26 procent van de jongeren van 13 tot 19 jaar, tien jaar later was dat nog maar 9 procent. Het aandeel van de 20- tot 34-jarigen waarvoor dit geldt, daalde in dezelfde periode van 42 naar 19 procent.

Tegelijk is het gebruik van sociale media sterk gegroeid. Maar: „Op sociale media is maar een klein deel van de content die je ziet afkomstig van Nederlandse journalisten en ook op de grote videostreamingsdiensten domineert Amerikaans aanbod – met uitzondering van Videoland.’’

Eerder dit najaar waarschuwde het Commissariaat al dat jongeren door het sterk gegroeide gebruik van sociale media „de waardevolle en kwalitatieve informatie die nieuwsmerken te bieden hebben niet meer tegenkomen of gebruiken, terwijl ongecheckte, ongeredigeerde berichten wel vrijelijk de ronde kunnen doen op sociale media”.

Televisiepakket

Al enkele jaren daalt het aantal mensen dat een abonnement heeft op een zogeheten ‘televisiepakket’ (een samengesteld aanbod van televisie- en radiozenders dat wordt geleverd door distributeurs als Ziggo, KPN en Delta). Daarnaast, of in plaats daarvan, zijn mensen abonnementen op streamingdiensten gaan afsluiten.

Weliswaar zijn er nog altijd meer gebruikers van een televisiepakket dan van streamingdiensten, maar er vindt een duidelijke verschuiving plaats. In de „leeftijdsgroep rond de dertig jaar die verhuist of het ouderlijk huis verlaat” nemen mensen vaker dan in andere leeftijdsgroepen géén abonnement meer op een televisiepakket, maar wél op een betaalde streamingdienst.

Inmiddels gebruikt ruim 70 procent van de ruim tweeduizend mensen die zijn ondervraagd voor de peiling van de Mediamonitor een betaalde streamingdienst – via een eigen abonnement dan wel met de inloggegevens van iemand anders. In de groep 20 tot 34 jaar gebruikt bijna tweederde zelfs meer dan twee streamingdiensten.

De populairste streamingdienst in Nederland is Netflix, waarvan bijna twee derde van de ondervraagden gebruik maakt. Op de tweede plaats staat Videoland, waar meer dan een kwart van de Nederlanders gebruik van maakt.

Videoland is onderdeel van RTL Nederland, waarop mediabedrijf DPG (in Nederland eigenaar van onder meer het AD, de Volkskrant en Qmusic) in december vorig jaar een bod uitbracht van 1,1 miljard euro. Die overname wacht nog op goedkeuring van de Autoriteit Consument en Markt, die zich over de mogelijke gevolgen voor de pluriformiteit van het nieuwsaanbod laat adviseren voor het Commissariaat voor de Media.

Luister naar