‘Ik wil graag begrijpen hoe muziek werkt, en dit werpt daar licht op”, zegt Bas Cornelissen. Op 24 februari promoveerde de muziekonderzoeker op het proefschrift Measuring Musics, een wetenschappelijk wat onorthodoxe explosie van ideeën over het analyseren van muziek. Van alles komt er langs, van gregoriaanse gezangen tot Malinese djembéritmes, van ritmedriehoeken en melodievierkanten tot de roep van de zebravink en de mathematische muziek van Arvo Pärt. Niet alles is even diep uitgewerkt.
Lees ook
Zebravinken leren zingen van een robot in een universiteitslab
„Ik heb gekozen voor een onconventionele vorm”, erkent Cornelissen in zijn werkkamer in het Amsterdamse Universiteitstheater, waar kleurige plots aan de muur hangen, en het geluid van bouwwerkzaamheden het interview af en toe overstemt. Er is geen centrale these of een duidelijke lijn, en als in een muziekstuk zitten er tussen de langere delen korte interludes: losser geschreven hoofdstukken over kleinere projecten. Het leidde tot discussie bij de promotiebegeleiders, maar uiteindelijk kwam er toch goedkeuring.
De weg ernaartoe was al net zo veelkleurig, vertelt Cornelissen, die naast onderzoeker ook docent is, en een masteropleiding oude muziek (hoofdvak zang) volgt aan het Conservatorium van Amsterdam. Daarnaast zingt hij in een kamerkoor, bijvoorbeeld zaterdag 9 maart bij de Johannes Passion in Vianen.
„Eigenlijk wilde ik de culturele evolutie van taal onderzoeken. In de taalkunde doen ze lab-experimenten en computersimulaties van simpele modeltalen, met maar een paar ‘woorden’, om te begrijpen hoe die vervolgens evolueren.”
Als kind was Cornelissen nogal bèta-gericht: wiskunde en natuurkunde hadden zijn interesse, en daarnaast muziek. Taal kwam pas later. „Mijn enige plan is altijd geweest om wetenschapper te worden. Maar ik vond het promoveren zwaar. Ik liep eigenlijk helemaal vast.”
In een opwelling deed hij op het laatste moment auditie bij het Utrechts Conservatorium. „Toen ik onverwacht aangenomen werd, stond mijn leven op zijn kop. Maar toen ik mijn begeleider vertelde ‘ik stop ermee, ik ga zingen’, zei hij ‘waarom doe je niet allebei?’ Wat natuurlijk een idioot idee is. Maar voor mij werkte het.”
„Wetenschap is monomaan: je kunt altijd verder graven, je begrijpt nooit iets helemaal, en niets relativeert dat. Musiceren bood balans. Ook daar wil je alles zo goed mogelijk doen, maar daar zit een grens aan. Bij een uitvoering doe je wat je kunt in de tijd die er is, maar er zijn altijd praktische beperkingen. En soms stijg je boven jezelf uit. Dat vind ik er fijn aan.”
:format(webp)/s3/static.nrc.nl/wp-content/uploads/2024/03/07120742/data112534645-846946.jpg)
:format(webp)/s3/static.nrc.nl/wp-content/uploads/2024/03/07120741/data112534681-1ebf14.jpg)
Foto’s: Dieuwertje Bravenboer
Muziekverzamelingen
Na de ommezwaai gooide Cornelissen het onderzoek om naar de evolutie van muziek. Hij dook in muziekverzamelingen, onder andere die van kerkgezangen die wij het best kennen als gregoriaans.
„Gezangen in die traditie worden vanaf de negende eeuw gezongen in kerken en kloosters. Tot mijn verbazing waren er enorme datasets: tienduizenden gezangen. Ze hebben geen toonsoort, zoals moderne westerse muziek, maar iets dat ‘modus’ heet. Iemand zei: als je dat echt wilt snappen, moet je een paar jaar gregoriaans gaan zingen. Die tijd had ik niet, dus ik dacht: laten we kijken of we het met computers kunnen karakteriseren.”
Dat lukte, en hielp indirect om licht te werpen op een academische vraag: wat zijn de kleinste eenheden van evolutie in muziek? Bestaat er een soort basiseenheid voor de evolutie van muziek, net zoals de basenparen in dna of klanken in talen?
Het karakteriseren van de modus lukte voor de gezangen het best als je uitgaat van woordeenheden in plaats van notengroepjes met vaste lengte. „Dat sluit aan bij de discussie onder kenners, over de vraag of de gezangen zijn opgebouwd uit gerecyclede blokjes van noten, vaak gebaseerd op woorden in te tekst, of dat ze from scratch zijn gecomponeerd.”
Een interlude in het proefschrift gaat over ritme. Al eerder had de promotor Henkjan Honing ‘ritmedriehoeken’ ontwikkeld, een grafisch hulpmiddel om ritmes te analyseren. „Je kunt direct zien of er structuur in je ritmische data zit”, zegt Cornelissen, die de driehoeken gebruikte om westerse pianomuziek en Cubaanse salsa te analyseren, maar ook de roep van dieren, van zangvogels tot apen en walvissen. „Daarnaast zijn het ook gewoon heel mooie, rijke beelden.”
Lees ook
Waar komt ons gevoel voor muziek vandaan?
:format(webp)/s3/static.nrc.nl/wp-content/uploads/2024/03/07120743/data112534672-0a7d2a.jpg)
Melodievierkanten
Om op een vergelijkbare manier melodieën zichtbaar te maken, bedacht hij ‘melodievierkanten’, Hier kwamen verzamelingen volksmuziek van pas, afkomstig uit Ierse, Schotse, Duitse, Luxemburgse en verschillende Chinese en Native American muziekculturen.
In totaal zo’n 15.000 melodieën gingen door Cornelissens melodievierkantengenerator, wat dichtheidsplots oplevert die per traditie duidelijk verschillen. Op basis daarvan construeerde Cornelissen een stamboom van muziekgenres, gebaseerd op de onderlinge verschillen tussen de vierkanten. Die stamboom lijkt heel aardig te kloppen: de Ierse volksmuziek zit aan dezelfde loot als de Schotse, ver van de Chinese en Native American takken. Maar Cornelissen is ‘huiverig’ om daar te veel conclusies uit te trekken. Of je zo de echte evolutie van muziektradities kunt naspeuren, moet toekomstig onderzoek nog uitwijzen.
Het laatste hoofdstuk is een vreemde eend in de bijt. „In alle andere hoofdstukken maak ik muziek meetbaar met veel data. Hier analyseer ik één muziekstuk van Arvo Pärt.” De populaire Estse componist Pärt (1935) ontwikkelde een nieuwe compositietechniek, die hij tintinnabuli noemde, die hij het strengst toepaste in zijn muziekstuk Summa. Cornelissen: „Er zit een heel duidelijke wiskundige structuur achter. Zo wordt elke melodie vergezeld door een tintinnabuli-stem, een begeleidingsstem, waarvoor de keuze maar heel beperkt is.”
Pärt leeft weliswaar nog, maar weigert commentaar te geven op zijn muziek. Met stug puzzelen wist Cornelissen toch de tintinnabuli-regels af te leiden. „Het idee was om op grond van de regels te kijken of je het hele stuk kunt genereren. Dan kom je heel ver, tot op 3 procent van alle noten. Maar op het punt dat er verfijningen aangebracht worden, zijn er soms inconsistente noten. Wat betekent dat? Zijn het individuele variaties, keuzes van Pärt? Of, en dat vind ik een grappige mogelijkheid, was het gewoon een foutje van Pärt? Maar het kan natuurlijk ook dat er nog een regel bestaat waar ik nog niet opgekomen ben.”
Ritmedriehoeken
:format(webp)/s3/static.nrc.nl/wp-content/uploads/2024/03/07120744/data112530759-1bdd2e.jpg)
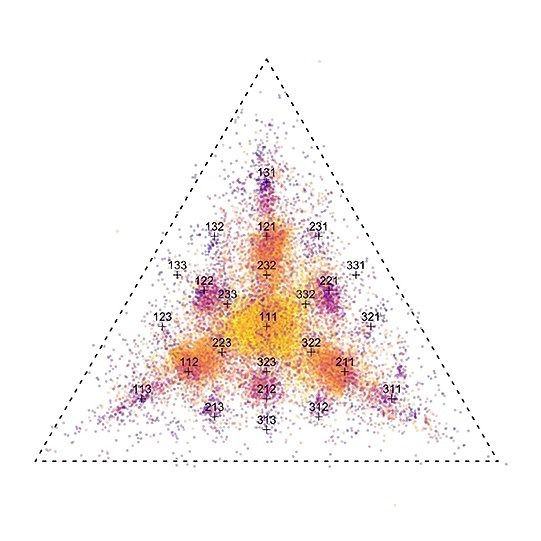
In een ritmedriehoek wordt een ritme van vier slagen weergegeven. Tussen die vier slagen zitten drie tijdsintervallen. Die intervallen (gedeeld door het totale tijdsinterval) worden geplot in een driehoek, waarbij de snelle ritmes een lichtere kleur krijgen dan de trage.
Een monotoon ritme belandt op die manier in het midden van de driehoek, een kort-kort-lang-ritme (1-1-2) ergens tussen het midden en een hoekpunt. Ritmes in veel muziekgenres hebben de neiging om in ratio’s van kleine gehele getallen op te treden. Zulke punten worden in de plots met kruisjes weergegeven. De plots kunnen gebruikt worden om muziek te analyseren, of om te zien wat er verandert als muzikanten voorgespeelde ritmes naspelen. Zo zien de driehoeken van Malinese drummers er heel anders uit dan die van Bulgaren, uit een muziektraditie met veel oneven ritmes, en die weer anders dan Cubaanse salsa.
Cornelissen: „Opvallend is dat de ritmes van professionele drummers vaak heel precies net naast de punten van kleinegetallenratio’s liggen.” Hij vermoedt dat de ritmes zo interessant blijven, en niet al te mechanisch klinken.
Melodievierkanten
:format(webp)/s3/static.nrc.nl/wp-content/uploads/2024/03/07120744/data112530765-42fb7c.jpg)
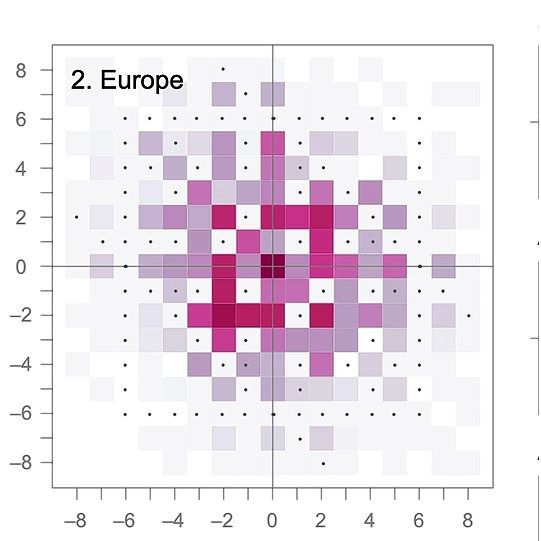
De melodieën worden opgehakt in groepjes van drie noten, en de twee intervallen daartussen worden uitgezet op de x- en y- as: een stijgend kwart, vijf halve toonafstanden, is +5. Daarna schuif je één noot op, en neem je het aanpalende groepje van drie.
Zo wordt een melodie een opeenvolging van punten in het vierkant. Sommige intervallen komen vaker voor, sommige zelden of nooit, afhankelijk van de muziektraditie. Cornelissen: „Het laat zien welke routes melodieën graag nemen in verschillende tradities.”
Zo is het kwart rechtsboven in de Amerikaanse muziekculturen nogal leeg, voor melodieën die inderdaad vaak dalen. In Schotse en Ierse muziek komen stijgende en dalende notendrietallen juist wel veel voor.
Arvo Pärts tintinnabuli
:format(webp)/s3/static.nrc.nl/wp-content/uploads/2024/03/07120745/data112530762-0f094d.jpg)
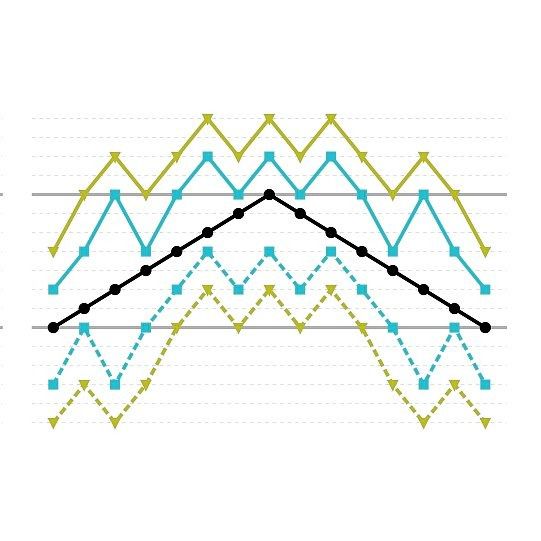
De melodielijn is de zwarte lijn in de grafiek. De mogelijke tintinnabuli-begeleidingsstemmen zijn gekleurd. In het stuk Summa mogen de begeleidingsnoten alleen uit één drieklank afkomstig zijn. De mag alleen in aanpalende stapjes bewegen, maar hij moet wel altijd bewegen, en hij moet onder de melodie blijven. Deze strenge regels bepalen vrijwel de hele begeleidingsstem.
